ACADEMIA DE MATEMATICAS







PROBLEMA




PROBLEMA
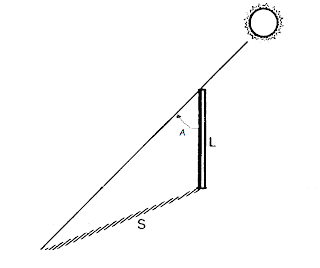
Con los datos que se te proporcionan, calcula la altura al elevarse un puente basculante

PROBLEMA




Calcula el ancho de una pantalla lcd teniendo como referencia que la mitad del largo de la pantalla mide 18.75cm y un triangulo con las medidas 11.45cm y 6cm


ANGULOS Y TIRMPOS: FORMA COMPLEJA E INCOMPLEJA
PROBLEMA
¿Que ángulos forman las agujas del reloj a las 2:10hrs?
Aguja del minutero avanza 6º/minutero= 6x minutos
Aguja hora avanza 0.5ª/minuto= 0.5x horas
6x-0.5x= 60
5.5x= 60
X= 60/5.5
X= 10.90
REFERENCIA ADICIONAL
http://www.kalipedia.com/matematicas-aritmetica/tema/angulos-reloj.html?x1=20070926klpmatari_404.Kes&x=20070926klpmatari_405.Kes
ELABORADO POR:
ARCE REYES LIZBETH LILIAN
FAUTSCH OROZCO VALERIA
 REFERENCIA ADICIONAL
REFERENCIA ADICIONAL
http://ieselpomar.juntaextremadura.net/curso%202008-2009/comenius%2008-09/RadioTerrestre.pdf
ELABORADO POR:
JORGE GONZALEZ SANCHEZ